
- #QUINE MCCLUSKEY ALGORITHM HOW TO#
- #QUINE MCCLUSKEY ALGORITHM PDF#
- #QUINE MCCLUSKEY ALGORITHM TRIAL#
Retrieved from ” https: The prime implicants are placed in row wise and min terms are placed in column wise. Digital Logic Circuit Analysis and Design. Mcfluskey These minterms are represented in a binary notation and combined as follows.
The K-map method doesn’t work well for functions of more than 4 variables because there is a limit on our ability to spot visual patterns in multidimensional space.
#QUINE MCCLUSKEY ALGORITHM HOW TO#
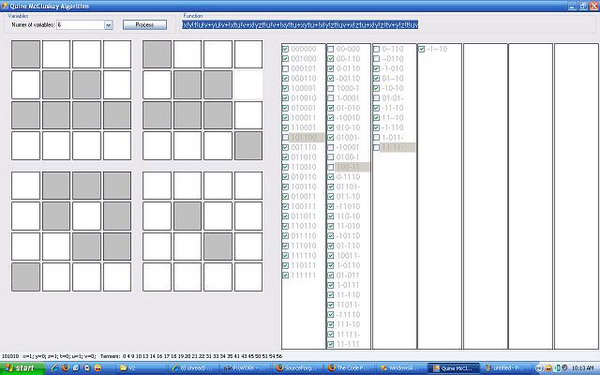
We’ll also learn how to analyze circuits that contain more than Column mccluskej shows minterms in binary form grouped in ascending order by the number of 1’s in the binary form of the minterm. The reduced table after removing the redundant rows is shown below. Looking at chart, some terms have not been checked off this is because they cannot possibly be combined with other terms, these terms are called prime implicants. The given Boolean function is in sum of min terms form. By combining terms 5 and 7, 6 and 7, 6 and 14, and 10 and 14, new terms are placed in column II.įirst, the group 0 term will be compared with all terms in group 1. The columns are labeled with the minterms in the on-set of the function. In previous chapter, we discussed K-map method, which is a convenient method for minimizing Boolean functions up to 5 variables. Everything About the Quine-McCluskey Method Um, where is the simple explanation of WHY anyone would want to use this?Ī prime implicant of a function F is a product term implicants which is no longer an implicants if any literal is deleted from it. The number of terms, however, is not minimum.
#QUINE MCCLUSKEY ALGORITHM PDF#
GRABADOS JAPONESES GABRIELE FAHR-BECKER PDF Everything About the Quine-McCluskey Method The don’t care terms are not placed on top-they are omitted from this section because they are not necessary inputs. With that being said, terms in adjacent groups only need to be compared. No matter when two terms are combined, the corresponding decimal numbers mccluske by a power of 2. January 11, by Donald Methdo In order to accurately use the Quine-McCluskey, the function needs to be given as a sum of minterms if the Boolean function is not in minterm form, the minterm expansion can be found to determine a minimum sum-of-products SOP expression for a function. In order to accurately use the Quine-McCluskey, the function needs to be given as a sum of minterms if the Boolean function is not in minterm form, the minterm expansion can be found to determine a minimum sum-of-products SOP expression for a function.

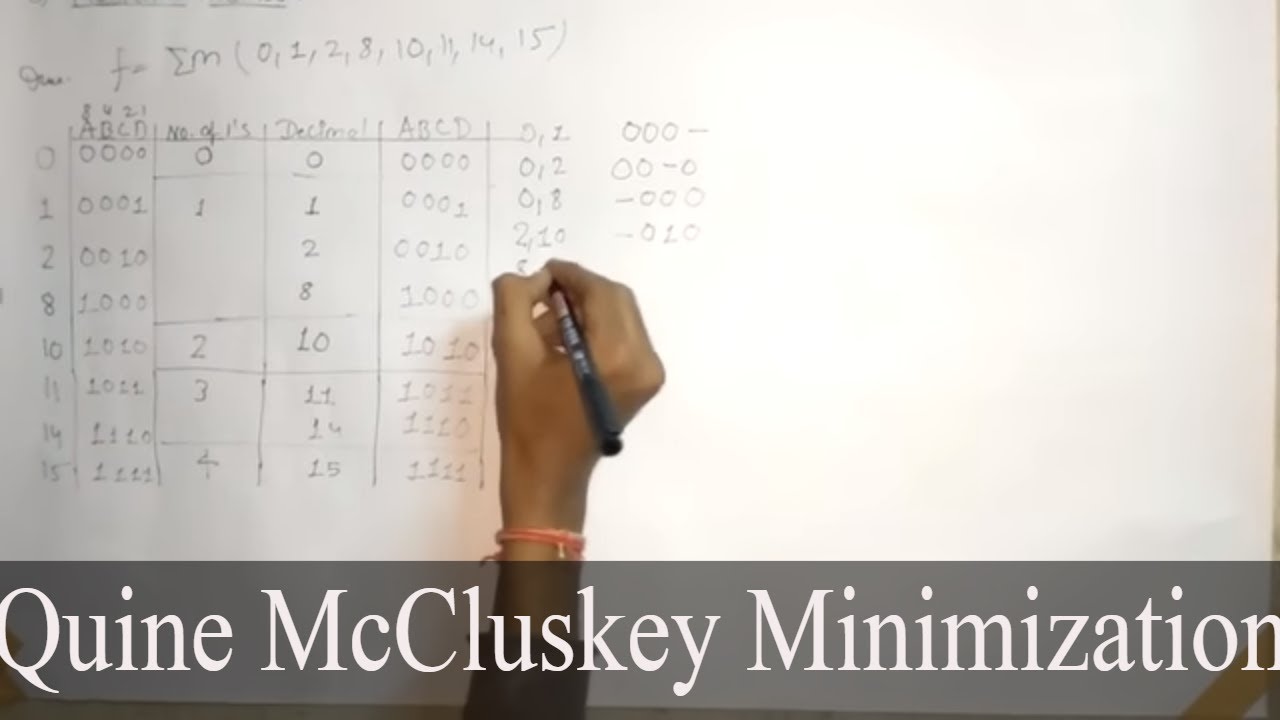
#QUINE MCCLUSKEY ALGORITHM TRIAL#
Mccluxkey simplest “additional procedure” is trial and error, but a more systematic way is Petrick’s method. The Quine-McCluskey algorithm or the method of prime implicants is a method used for minimization of Boolean functions that was developed by Willard V. Column 2 shows the minterm value written as a binary number. The given methd terms are arranged into 4 groups based on the number of ones present metnod their binary equivalents. Step two of the algorithm amounts to solving the set cover problem NP-hard instances of this problem may occur in this algorithm step. 21 Jan The Quine-McCluskey method is an exact algorithm which finds a minimum-cost This handout introduces the method and applies it to several. Digital Circuits Quine-McCluskey Tabular Method – Learn Digital Circuits in simple and easy steps starting from basic to advanced concepts with examples. The function that is minimized can be entered via a truth table that represents the function y = f(xn,x1, x0).


 0 kommentar(er)
0 kommentar(er)
